さて, 前回は群の定義についてやった. 今回は群の例についてやることにする.
まず, 前回の復習として群の定義を見てみよう.
(再掲)定義1 群の定義 まず, 集合![]() に二項演算
に二項演算![]() が定義されていて次の3つの条件を満たすとき集合
が定義されていて次の3つの条件を満たすとき集合![]() を群という.
を群という.
注意1 当たり前ではあるが, ![]() の2元
の2元![]() ,
,![]() に対し
に対し![]() でなければ二項演算が定義されているとはいえないのでこの点をまず確かめること.
でなければ二項演算が定義されているとはいえないのでこの点をまず確かめること.
(1) ∀![]() に対し,
に対し, ![]() が成立する.(結合法則).
が成立する.(結合法則).
(2) ∃![]() , ∀
, ∀![]() に対し,
に対し, ![]() であるような元
であるような元![]() がある.(単位元の存在).
がある.(単位元の存在).
(3) ∀![]() に対し, ∃
に対し, ∃![]() で
で![]() が成立する.(逆元の存在。逆元
が成立する.(逆元の存在。逆元![]() を
を![]() と書くことが多い).
と書くことが多い).
このとき, 集合![]() を群と呼ぶ.
を群と呼ぶ.
記法, 記号等の追加.
(Q.E.D) 証明終了.
![]() 集合Aから集合Aの要素Bを除いた集合.
集合Aから集合Aの要素Bを除いた集合.
では, さっそく群の例についてやってみよう.
例2 ![]() を
を![]() (
(![]() から0を除いた集合)とし, 演算を乗法とすると
から0を除いた集合)とし, 演算を乗法とすると![]() は群である.
は群である.
証明 ) 群の定義それぞれについて成立することを示せばよい.
もちろん, ![]() に対し
に対し ![]() である.
である.
まず, (1)について.
∀![]() をとる. このとき,
をとる. このとき, ![]() であることを示す.
であることを示す.
まず, ![]() (
(![]() )とおける.
)とおける.
![]()
また,![]() .
.
したがって, 結合法則が成立する.
次に, (2)について.
∃![]() , ∀
, ∀![]()
![]() であることを示す.
であることを示す.
演算は乗法なので, ![]() .
.
![]() となり,
となり, ![]() が任意であることから
が任意であることから![]() となる.
となる.
もちろん, ![]() であるので(2)も成立する.
であるので(2)も成立する.
最後に(3)について.
∀![]() , ∃
, ∃![]()
![]() であることを示す.
であることを示す.
(2)より![]() であるから
であるから![]() となり,
となり, ![]() より
より ![]() である.
である.
したがって, 両辺を![]() で割ると
で割ると ![]() (
(![]() ) である.
) である.
もちろん, ![]() であるから(3)も成立する.
であるから(3)も成立する.
以上より, ![]() は群である.
は群である.
同様に, ![]() や
や![]() も群である.
も群である.
例3 ![]() を
を![]() から0を除いた集合とし, これを
から0を除いた集合とし, これを![]() とおく. このとき,
とおく. このとき, ![]() は乗法に関して群となる.
は乗法に関して群となる.
証明)まず, (1)について.
∀![]() に対し,
に対し, ![]() とおく.
とおく.
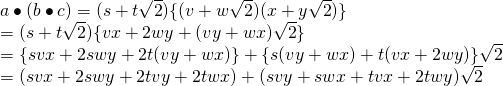
また,
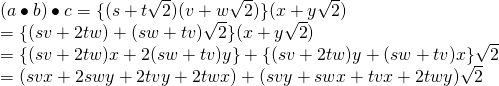
よって, (1)の結合法則が成立.
次に(2)について.
∃![]() , ∀
, ∀![]() ,
, ![]() を示す.
を示す.
![]() とおく. このとき,
とおく. このとき, ![]() .
.
![]() より,
より, ![]() .
.
よって, ![]() ,
, ![]() .
.
これを計算して, ![]() となり
となり ![]() .
.
最後に(3)について.
∀![]() , ∃
, ∃![]() ,
, ![]() .
.
今, (2)より![]() であるから
であるから ![]()
![]() とおくと
とおくと ![]() .
.
![]() なので, 両辺を
なので, 両辺を![]() で割って
で割って ![]() .
.
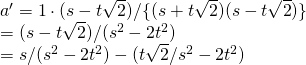 .
.
よって, ![]() である.
である.
以上より, ![]() は乗法に関して群となる. (Q.E.D)
は乗法に関して群となる. (Q.E.D)
例4 ![]() は乗法に関して群をなす. ここで
は乗法に関して群をなす. ここで![]() は実数を成分とする
は実数を成分とする![]() 次正則行列全体の集合である.
次正則行列全体の集合である.
証明) ![]() とすると,
とすると, ![]() ・・・(Ⅰ)
・・・(Ⅰ)
(Ⅰ) ![]() の行列式を
の行列式を![]() とすると,
とすると, ![]() である.
である.
今, ![]() より
より![]() で
で![]() より
より![]() である.
である.
よって, ![]() である.
である.
次に(1)について
∀![]() のとき
のとき ![]() である.
である.
以下証明のアイデアのみ述べる.
![]() の場合は自明.
の場合は自明.
![]() の場合
の場合 ![]() の成分を文字で置き, 積を計算すればよい.
の成分を文字で置き, 積を計算すればよい.
![]() が一般のとき
が一般のとき ![]() を
を![]() のようにおいて積の定義から計算するとよい.
のようにおいて積の定義から計算するとよい.
詳しくは線形代数の本等を参照のこと.
また, ![]() を一般線形群と呼ぶ.
を一般線形群と呼ぶ.
次に(2)について.
∀![]() に対し,
に対し, ![]() となる行列
となる行列![]() が存在しこれを
が存在しこれを![]() 次単位行列という.
次単位行列という.
よって(2)が成立する.
最後に(3)について.
![]() が正則なので, ∀
が正則なので, ∀![]() に対し∃
に対し∃![]()
![]() となる.
となる.
したがって, (3)も成立する.
ではここで, 1つ問題です.
問題 集合![]() に対し演算を
に対し演算を![]() つまり,
つまり, ![]() を13で割った余りで定める. このとき次の問いに答えよ.
を13で割った余りで定める. このとき次の問いに答えよ.
(1) ![]() の単位元を求めよ.
の単位元を求めよ.
(2)逆元をもつ![]() の元をすべて求めよ.
の元をすべて求めよ.
(3) Aは二項演算![]() によって群となるか.
によって群となるか.
では少し考えてみましょう.
解答(略解)
(1) 前にやった例と同じである. ![]() を解き
を解き![]() を得る.
を得る. ![]() より単位元は1.
より単位元は1.
(2) ![]() なので高々元は12個しかない. ではそれぞれについて計算する.
なので高々元は12個しかない. ではそれぞれについて計算する.
まず1について, ![]() であるので1が逆元となる.
であるので1が逆元となる.
2について, ![]() より7が逆元となる.
より7が逆元となる. ![]() .
.
3について, ![]() より9が逆元となる.
より9が逆元となる. ![]() .
.
4について, ![]() より10が逆元となる.
より10が逆元となる. ![]() .
.
5について, ![]() より8が逆元となる.
より8が逆元となる. ![]() .
.
6について, ![]() より11が逆元となる.
より11が逆元となる. ![]() .
.
7について, 先ほどのことより2が逆元となる.
8について, 同様に5が逆元となる.
9について, 3が逆元となる.
10について, 4が逆元となる.
11について, 6が逆元となる.
12について, ![]() より12が逆元となる.
より12が逆元となる.
注意 ![]() がcで割り切れるとき,
がcで割り切れるとき, ![]() と表す.
と表す.
これは別の言い方をすると, ![]() と
と![]() は
は![]() で割ったあまりが等しいということになる.
で割ったあまりが等しいということになる.
(3)
群の定義(1)について
![]() を13で割ったあまりは1~12のいずれかである. なぜなら13は素数なので12までの数どうしをかけても13の倍数にはならない. よって余りが0になることはない.
を13で割ったあまりは1~12のいずれかである. なぜなら13は素数なので12までの数どうしをかけても13の倍数にはならない. よって余りが0になることはない.
したがって, ![]() のとき,
のとき, ![]() である.
である.
群の定義(2)について
![]()
![]() より
より ![]() で考えたときの値は等しい.
で考えたときの値は等しい.
群の定義(3)について (1)で確認したので成立しますね.
群の定義(4)について (2)で確認したので成立しますね.
以上から![]() は二項演算
は二項演算![]() で群となる.
で群となる.
参考文献
[1] 群論 芝浦工業大学
[2] 代数学Ⅱ 弘前大学
